Sistemas Numéricos

Sistema Numérico Decimal

El sistema de numeración decimal es un sistema posicional.  En este sistema utilizamos diez dígitos, que son: 0, 1, 2, 3, 4, 5, 6, 7, 8, y 9. Por ello decimos que el sistema decimal es de base diez. 

En este sistema, cada cifra representa un valor distinto dependiendo de su ubicación en el número.

Esto quiere decir que el principio de agrupamiento de este sistema es diez, en donde cada 10 unidades se forma otra de carácter superior, la cual se escribe a la izquierda de la primera de las unidades. Esto es ilustrado en el ábaco, en donde cada vez que tenemos 10 fichas en una varilla, las transformamos en una de la varilla inmediatamente izquierda y la ubicamos en ésta, con lo cual obtenemos que 10 unidades equivales a una decena, que 10 decenas equivalen a 1 centena y así sucesivamente.

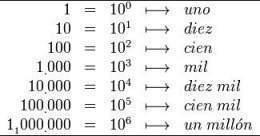
Sistema Numérico Binario

El sistema de numeración binario utiliza sólo dos dígitos, el cero (0) y el uno (1).

En una cifra binaria, cada dígito tiene distinto valor dependiendo de la posición que ocupe. El valor de cada posición es el de una potencia de base 2, elevada a un exponente igual a la posición del dígito menos uno. Se puede observar que, tal y como ocurría con el sistema decimal, la base de la potencia coincide con la cantidad de dígitos utilizados (2) para representar los números.

De acuerdo con estas reglas, el número binario 1011 tiene un valor que se calcula así:

1*2³ + 0*2² + 1*2¹ + 1*2⁰ , es decir:

8 + 0 + 2 + 1 = 11

y para expresar que ambas cifras describen la misma cantidad lo escribimos así:

1011₂ = 11₁₀

Sistema Numérico Octal

El sistema octal es un sistema de numeración posicional de base 8.

Los símbolos que se usan en este sistema son:

0, 1, 2, 3, 4, 5, 6, 7

• 13(8 = 11(10

• 25(8 = 21(10

• 1077(8 = 575(10

1. Dividimos el número entre 8:

1. Si el cociente es mayor o igual que 8, lo dividimos entre 8.En nuestro caso, el cociente es 96 (mayor que 8), por lo que lo dividimos de nuevo:

1. Continuamos así hasta obtener un cociente menor que 8.En nuestro caso, el cociente es 12 (mayor que 8), así que lo dividimos de nuevo:

1. El número en base 8 es:(Último cociente) (Último resto) (Penúltimo resto)… (Segundo resto) (Primer resto).

• El último cociente es 1.

• El último resto es 4.

• El penúltimo resto es 0.

• El primer resto es 0.

Para indicar que un número está escrito en base 8, usamos el subíndice (8,  y para indicar que un número está escrito en base 10, usamos el subíndice (10.

Ejemplos:

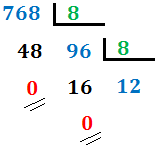
A continuación, explicamos el método para pasar del sistema decimal al sistema octal mediante un ejemplo. Escribiremos el número 768(10 en base 8:

1. 

1. 

1. 
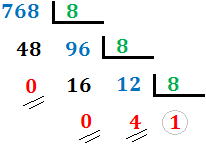   El cociente es 1, menor que 8, con lo que hemos terminado el proceso. Hemos indicado los restos con dos rayas y el último cociente con una circunferencia.

En nuestro caso,

Por tanto, el número 768 en base octal es 1400. Es decir,

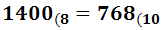
Sistema Numérico Hexadecimal

El sistema hexadecimal es el sistema de numeración posicional que tiene como base el 16. Sus números están representados por los 10 primeros dígitos de la numeración decimal, y el intervalo que va del número 10 al 15 están representados por las letras del alfabeto de la ‘A’ a la ‘F’.

Su uso actual está muy vinculado a la informática y ciencias de la computación donde las operaciones de la CPU suelen usar el byte u octeto como unidad básica de memoria. Aunque los circuitos electrónicos digitales y las computadoras utilizan el sistema binario, el trabajar con este sistema de numeración es bastante más complicado, lo que da como resultado una gran posibilidad de cometer errores se trabaja con números binarios demasiado largos.

Este sistema posee dos grandes ventajas en el entorno informático:

• Crea una simplificación en la escritura de los números decimales, ya que cada 4 cifras binarias se representa simplemente por una hexadecimal.
• Cada cifra hexadecimal se puede expresar por 4 cifras binarias, con lo que la transposición entre estos dos sistemas se facilita considerablemente. Para convertir un numero binario a hexadecimal se realizará el mismo proceso pero de forma inversa.