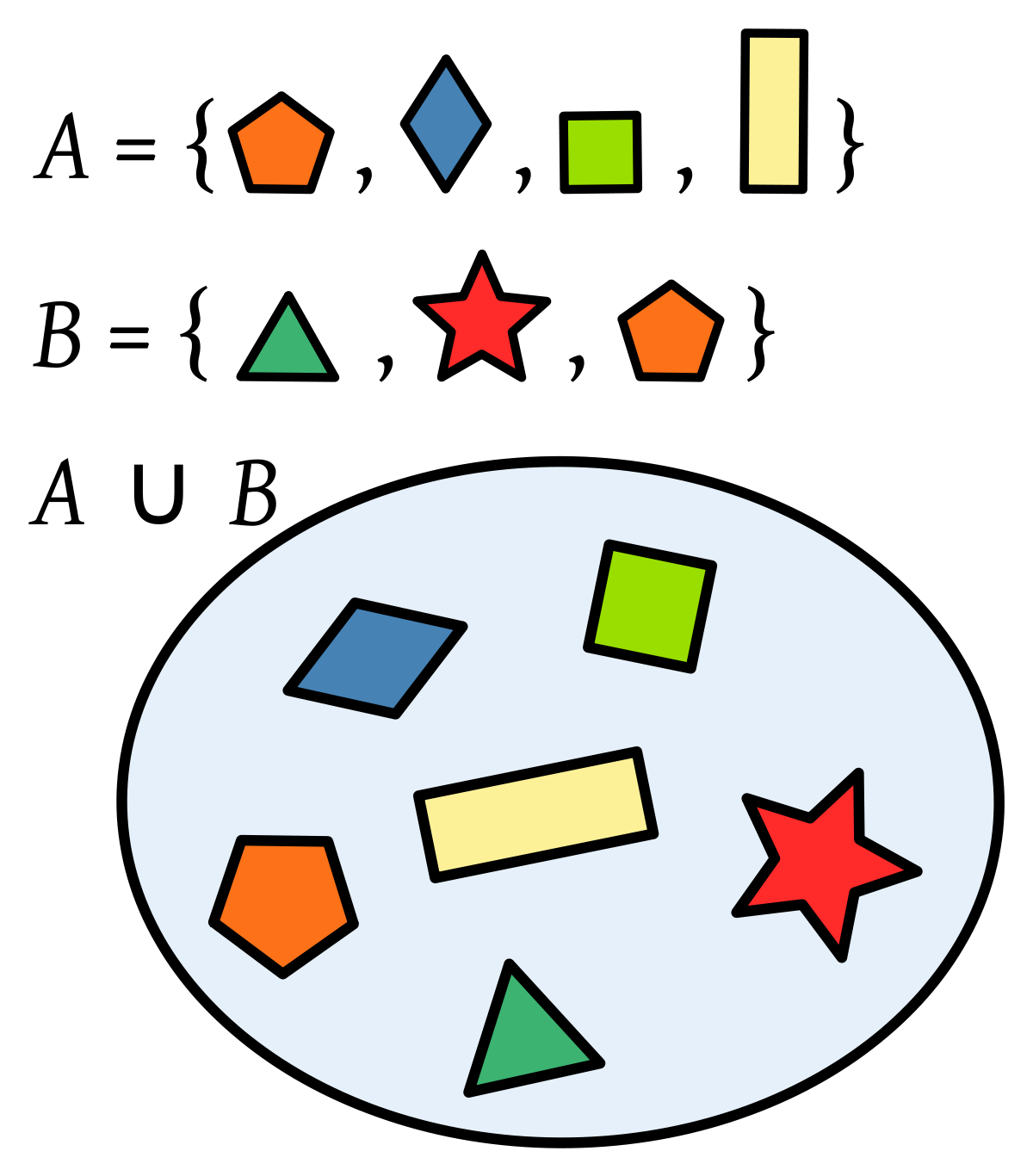
Conjuntos de unión

conjuntos de unión

Conjuntos

1. ¿Qué es conjunto?

Un conjunto se define como la agrupación de diferentes elementos que comparten entre sí características y propiedades semejantes. Estos elementos pueden ser cualquier cosa, tales como números, canciones, meses, personas, etcétera.

A su vez un conjunto puede convertirse también en un elemento. Por ejemplo, un ramo de flores. En principio una flor sería el primer elemento, pero al conjunto de flores se lo puede considerar luego como un ramo de flores, convirtiéndose así, en un nuevo elemento.

2. Tipos de conjuntos

A la hora de formar un conjunto, la manera y el por que de como los agrupamos puede variar, dando lugar entonces a los diferentes tipos de conjuntos:

• Conjuntos finito: La característica de este conjunto es que sus elementos pueden ser contar o enumerar en su totalidad. Por ejemplo, los meses del año establecen un conjunto finito: enero, febrero, marzo, abril, mayo, junio, julio, agosto, septiembre, octubre, noviembre y diciembre.
• Conjunto infinito: Un conjunto será infinito cuando sus elementos sean imposibles de contar o enumerar en su totalidad, debido a que no tienen fin. Los números son un claro ejemplo de un conjunto infinito.
• Conjunto unitario: Aquel que está compuesto por un único elemento. La luna se encuentra dentro de este conjunto, pues es el único satélite natural del planeta tierra.
• Conjunto vacío: se trata de un conjunto el cual no presenta ni tiene elementos.
• Conjunto homogéneo: Conjuntos cuyos elementos presentan una misma clase o categoría.
• Conjunto heterogéneo: Los elementos de estos conjuntos difieren en clase y categoría.
• Conjuntos equivalentes: Serán equivalentes aquellos conjuntos cuya cantidad de elementos sea la misma.
• Conjuntos iguales: Podrá decirse que dos o más conjuntos son iguales, cuando estén compuestos por elementos idénticos.

Nombre en números binarios

divicion de números binarios

Es muy simple realizar una división de números binarios pues es sumamente similar a la división con números decimales. Hay un cociente como resultado con un posible residuo, hay un dividendo y un divisor y se trata de encontrar múltiplos e ir los restando uno por uno. No creo necesario extenderse en la explicación paso a paso de la división de números enteros positivos en binario. Basta con un pequeño ejemplo y recordar las reglas para la división de números decimales ya que son iguales.

División de números binarios

La división en binario es similar a la decimal, la única diferencia es que a la hora de hacer las restas, dentro de la división, estas deben ser realizadas en binario. Por ejemplo, vamos a dividir 100010010 (274) entre 1101 (13):

 100010010 |1101
            ——————
- 0000      010101
———————
 10001
- 1101
———————
  01000
 - 0000
 ———————
   10000
  - 1101
  ———————
    00111
   - 0000
   ———————
     01110
    - 1101
    ———————
     00001

Multiplicación de números binarios

Para la multiplicación de números binarios utilizaremos las mismas reglas que para la multiplicación de números decimales. La tabla de multiplicar es mucho mas sencilla ya que solo tiene dos entradas 0 y 1.Si procedemos igual que en decimal una multiplicación resultaría:


         010011
         101101
         ------
         010011
        000000
       010011
      010011
     000000
    010011
    -----------
    01101010111

De esta forma deben sumarse muchos bits simultaneamente por columna. En nuestro caso hay una columna de seis bits, dos de cinco, cuatro, tres, dos y uno; sin contar los bits de transporte ( carry ) de las columnas anteriores.
En general los sumadores que dispondremos en las computadoras son capaces de sumar dos números por lo tanto debemos adoptar el algoritmo e ir acumulando el resultado parcial y sucesivamente sumar el multiplicando corrido si el bit del multiplicador asi lo indica.


                      010011
                      101101
                      ------
                      000000
                      010011
                      ------
                      010011
                     000000
                     -------
                      0010011
                     010011
                     --------
                     01011111
                    010011
                    ---------
                    011110111
                   000000
                   ----------
                   0011110111
                  010011
                  -----------
                  01101010111

Una primera conclusión es que aunque se multiplican dos números de 6 bits y el resultado es de 12 bits ( en general los dos números de n bits y el resultado de 2n bits ) no hace falta un sumador de 12 bits si se cuenta con un sumador de 6 bits que se corre un lugar para la izquierda.
El mismo efecto se consigue si se mantiene fijo el sumador y el multiplicando y se corre el resultado acumulado a la derecha un bit cada vez.
La configuración mas sencilla consiste en un acumulador de 2n bits, separado en dos registros de n bits. El de la izquierda contiene cero en todos sus bits al comenzar y en el se almacenan las sumas parciales; el de la derecha al comenzar contiene el multiplicador y la unidad puede detectar si el último bit vale 0 o 1.
Luego de cada suma se corre el acumulador un lugar a la derecha, ingresando el bit de carry. De esta forma los sucesivos bits del multiplicador estan ubicados en el último bit del registro y eso le permite a la unidad decidir si sumar el multiplicando o cero. De esta forma la unidad pierde el valor del multiplicador y al final el resultado esta en los 2n bits del acumulador.

Resta de números Binarios

Resta de números binarios

El algoritmo de la resta en binario es el mismo que en el sistema decimal. Pero conviene repasar la operación de restar en decimal para comprender la operación binaria, que es más sencilla. Los términos que intervienen en la resta se llaman minuendo, sustraendo y diferencia.
Las restas básicas 0-0, 1-0 y 1-1 son evidentes:

• 0 - 0 = 0
• 1 - 0 = 1
• 1 - 1 = 0
• 0 - 1 = no cabe o se pide prestado al próximo.

La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada de la posición siguiente: 10 - 1 = 1 y me llevo 1, lo que equivale a decir en decimal, 2 - 1 = 1. Esa unidad prestada debe devolverse, sumándola, a la posición siguiente. Veamos algunos ejemplos:

Restamos 17 - 10 = 7 (2=345)          Restamos 217 - 171 = 46 (3=690)
        10001                           11011001    
       -01010                          -10101011
       ——————                          —————————
        01111                           00101110

A pesar de lo sencillo que es el procedimiento, es fácil confundirse. Tenemos interiorizado el sistema decimal y hemos aprendido a restar mecánicamente, sin detenernos a pensar en el significado del arrastre. Para simplificar las restas y reducir la posibilidad de cometer errores hay varias soluciones:

• Dividir los números largos en grupos. En el siguiente ejemplo, vemos cómo se divide una resta larga en tres restas cortas:

        100110011101             1001     1001     1101
       -010101110010            -0101    -0111    -0010
       —————————————      =     —————    —————    —————
        010000101011             0100     0010     1011

Suma de números binarios