producto cartesiano

En matemáticas, el producto cartesiano de dos conjuntos es una operación, que resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse de forma que el primer elemento del par ordenado pertenezca al primer conjunto y el segundo elemento pertenezca al segundo conjunto.

El producto cartesiano recibe su nombre de René Descartes, cuya formulación de la geometría analítica dio origen a este concepto.

Ejemplo[editar]

Por ejemplo, dados los conjuntos:

${\displaystyle A=\{1,2,3,4\}}$

y

${\displaystyle B=\{a,b\}}$

su producto cartesiano de A por B es:

${\displaystyle {\begin{array}{r|cccc}b&(1,b)&(2,b)&(3,b)&(4,b)\\a&(1,a)&(2,a)&(3,a)&(4,a)\\\hline A\times B&1&2&3&4\\\end{array}}}$

que se representa:

${\displaystyle A\times B=\{(1,a),(1,b),(2,a),(2,b),(3,a),(3,b),(4,a),(4,b)\}}$

y el producto cartesiano de B por A es:

${\displaystyle {\begin{array}{r|cc}4&(a,4)&(b,4)\\3&(a,3)&(b,3)\\2&(a,2)&(b,2)\\1&(a,1)&(b,1)\\\hline B\times A&a&b\\\end{array}}}$

que se representa:

${\displaystyle B\times A=\{(a,1),(a,2),(a,3),(a,4),(b,1),(b,2),(b,3),(b,4)\}}$

Ver que:

${\displaystyle (1,a)\neq (a,1)}$

Dado que son pares ordenados.

Definición[editar]

Un par ordenado es una colección de dos objetos distinguidos como primero y segundo, y se denota como (a, b), donde a es el «primer elemento» y b el «segundo elemento». Dados dos conjuntos A y B, su producto cartesiano es el conjunto de todos los pares ordenados que pueden formarse con estos dos conjuntos:

El producto cartesiano de A y B es el conjunto A × B cuyos elementos son los pares ordenados (a, b), donde a es un elemento de A y b un elemento de B: ${\displaystyle A\times B=\{(a,b):a\in A\;\;{\text{y}}\;\;b\in B\}}$

Puede definirse entonces el cuadrado cartesiano de un conjunto como A² = A × A.

El conjunto Z² puede visualizarse como el conjunto de puntos en el plano cuyas coordenadas son números enteros.

Ejemplos[editar]

Números enteros

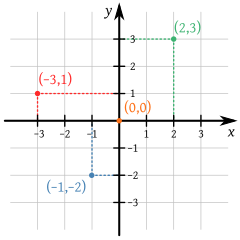
Sea también el conjunto de todos los números enteros Z = {..., −2, −1, 0, +1, +2, ...}. El producto cartesiano de Z consigo mismo es Z² = Z × Z = { (0,0), (0, +1), (0, −1), (0, +2), ..., (+1, 0), ... (−1, 0), ... }, es decir, el conjunto de los pares ordenados cuyos componentes son enteros. Para representar los números enteros se utiliza la recta numérica, y para representar el conjunto Z² se utiliza un plano cartesiano (en la imagen).

Pintura y pinceles

Sean los conjuntos T de tubos de pintura, y P de pinceles:

${\displaystyle T=\{\,}$

,

,

,

${\displaystyle \}\,}$

${\displaystyle P=\{\,}$

,

,

,

,

${\displaystyle \}\,}$

El producto cartesiano de estos dos conjuntos, T × P, contiene todos los posibles emparejamientos de pinceles y tubos de pintura. De manera similar al caso de un plano cartesiano en el ejemplo anterior, este conjunto puede representarse mediante una tabla: